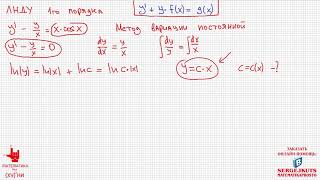КАК ДОКАЗАТЬ ЧТО ФУНКЦИЯ ОБРАТИМА
Для доказательства, что функция обратима, необходимо выполнить несколько шагов:
1. Докажите, что функция является инъективной. Для этого предположим, что у нас есть два разных значения x₁ и x₂ в области определения функции, которые отображаются на одно и то же значение в области значений функции. Показав, что это предположение неверно, мы можем установить инъективность функции.
2. Докажите, что функция является сюръективной. Для этого необходимо показать, что для любого значения y в области значений функции существует значение x в области определения функции, такое что f(x) = y.
3. Докажите, что функция является ограниченной. Для этого нужно установить, что существуют константы а и b, такие что для любого значения x в области определения функции, a ≤ f(x) ≤ b.
4. Докажите, что функция является непрерывной. Для этого можно использовать определение непрерывности, доказывая, что для любого эпсилон больше нуля существует дельта больше нуля, такое что если |x - c| < дельта, то |f(x) - f(c)| < эпсилон.
Если все эти условия выполняются, то можно сделать вывод, что функция обратима.
Обратная функция. Практическая часть. 10 класс.
Функции — Принципы математического мышления — уровень 3 из 5
Обратная функция. 10 класс.
Свойства функции. Четность и нечетность функции. 10 класс.
ВЗАИМНО ОБРАТНЫЕ ФУНКЦИИ
10 класс, 10 урок, Обратная функция