КАК СДВИГАЕТСЯ ГРАФИК ФУНКЦИИ В ЗАВИСИМОСТИ ОТ КОЭФФИЦИЕНТОВ
График функции может сдвигаться в зависимости от коэффициентов, которые влияют на ее общий вид и положение на координатной плоскости.
При изменении коэффициента при основной переменной функции (обычно x) происходит горизонтальное смещение графика. Положительное значение коэффициента приводит к сдвигу вправо, в то время как отрицательное значение - к сдвигу влево.
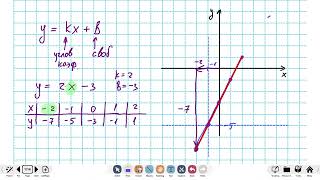
Коэффициент, умножающийся на переменную в функции (например, a*x), изменяет наклон графика. Если значение коэффициента a больше 1, график будет становиться более крутым, а при значении меньше 1 - менее крутым. При отрицательном значении a график отображается в зеркальном отражении относительно оси x.
Вертикальный сдвиг графика функции происходит за счет коэффициента, добавляемого к функции (например, f(x) + b). Положительное значение b приводит к сдвигу вверх, а отрицательное - вниз.
Также следует обратить внимание на коэффициенты в функциях, задающих форму графика, такие как степенные функции, экспоненциальные функции, логарифмические функции и т. д. Изменение этих коэффициентов может привести к существенным изменениям в форме и положении графика функции.
Как построить график функции без таблицы
Линейная функция: краткие ответы на важные вопросы - Математика - TutorOnline
Графики функций - сдвиги гиперболы и нахождение коэффициентов
Преобразование графиков функций. Сжатие и растяжение. 10 класс.
Как легко составить уравнение параболы из графика
ГРАФИК ФУНКЦИЙ — Сдвиги Графика Функции, Как строить Графики Функции // Алгебра 8 класс