Как Решать Кусочно Линейные Функции

Кусочно линейные функции представляют собой функции, которые определены на разных интервалах и заданы линейными выражениями на каждом из этих интервалов. Решение таких функций можно разбить на несколько шагов.

Шаг 1: Определение интервалов. Необходимо определить все интервалы, на которых функция задана линейными выражениями. Это позволит разбить область определения функции на несколько частей, на каждой из которых функция будет задана линейным уравнением.

Шаг 2: Нахождение уравнений. Для каждого интервала определения функции необходимо найти линейное уравнение, описывающее функцию на этом интервале. Для этого можно использовать уже заданные точки на графике функции или условия, заданные в задаче.

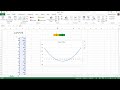
Шаг 3: Построение графика. После того как уравнения для каждого интервала определены, можно построить график функции, соединяя точки на каждом интервале, соответствующие найденным уравнениям.

Шаг 4: Анализ промежутков. Важно проанализировать свойства функции на каждом интервале, например, наличие экстремумов или точек разрыва. При необходимости можно определить значения функции в этих точках и дополнить график.

Таким образом, решение кусочно линейных функций сводится к определению интервалов, нахождению уравнений, построению графика и анализу свойств функции на каждом интервале. Это позволяет получить представление о поведении функции на всей области определения.