Как Разложить Функцию На Множители

Разложение функции на множители является важным понятием в математике. Это процесс преобразования заданной функции в произведение более простых функций.

Существует несколько методов разложения функций на множители. Один из самых распространенных методов - использование теоремы о промежуточных значениях. Согласно этой теореме, если функция принимает два различных значения на двух различных точках отрезка, то она принимает все значения между этими точками. Используя это свойство, мы можем найти корни функции и разложить ее на линейные множители.

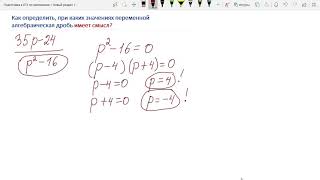
Другой метод разложения функции на множители - использование формулы разложения квадратного трехчлена. Если функция представляет собой квадратный трехчлен, то ее можно разложить на множители, используя формулу разложения. Этот метод часто применяется при работе с квадратными функциями.

Еще одним методом является использование метода группировки множителей. Если функция представляет собой разность или сумму двух членов, то мы можем использовать метод группировки множителей для их разложения на множители. Этот метод особенно полезен при работе с многочленами.

Важно отметить, что разложение функции на множители позволяет упростить заданную функцию и найти ее корни. Оно также помогает в анализе поведения функции и решении уравнений.