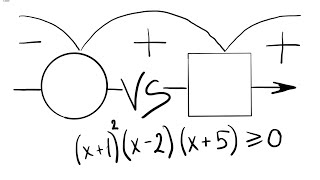Как Определить Возрастание И Убывание Функции По Формуле

Для определения возрастания и убывания функции по формуле необходимо анализировать ее производную. Возьмем функцию f(x) и найдем ее производную f'(x).

Если производная положительна на определенном интервале, то функция возрастает на этом интервале. Если же производная отрицательна на интервале, то функция убывает на этом интервале.

Для определения точек возрастания и убывания функции, найдем корни производной f'(x) по формуле f'(x) = 0. Полученные значения x являются точками, где функция меняет свой характер (от возрастания к убыванию или наоборот).

Итак, если производная f'(x) больше нуля на интервале A, B, то функция f(x) возрастает на этом интервале. Если же f'(x) меньше нуля на интервале C, D, то функция f(x) убывает на этом интервале.

Например, рассмотрим функцию f(x) = x^2 - 3x + 2. Найдем производную функции f'(x) = 2x - 3. Чтобы определить, когда функция возрастает или убывает, приравняем f'(x) к нулю и решим уравнение: 2x - 3 = 0. Получаем x = 3/2. Теперь анализируем интервалы:

Если x < 3/2, то f'(x) < 0, следовательно, функция f(x) убывает на интервале (-∞, 3/2);
Если x > 3/2, то f'(x) > 0, следовательно, функция f(x) возрастает на интервале (3/2, +∞).

Таким образом, мы определили, когда функция возрастает и убывает по формуле. Этот метод можно применить и для других функций, используя анализ производной и ее нулей.