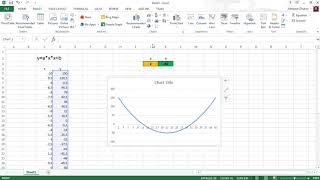
Как По Дифференциальному Уравнению Звена Найти Его Переходную Функцию

Переходная функция звена определяется путем решения соответствующего дифференциального уравнения. Для того чтобы найти переходную функцию, необходимо знать дифференциальное уравнение, описывающее поведение звена во временной области.

Переходная функция представляет собой математическую модель, которая описывает динамические свойства звена. Она позволяет определить, как система реагирует на входные сигналы во времени.

Для нахождения переходной функции звена, нужно вначале определить его дифференциальное уравнение. В зависимости от типа звена это уравнение может иметь различный вид. Некоторые типы звеньев, такие как интегрирующие или дифференцирующие, имеют простые дифференциальные уравнения, которые можно легко решить.

Определенное дифференциальное уравнение звена может быть линейным или нелинейным. Линейные уравнения, как правило, проще решать и дают аналитическое выражение для переходной функции. В случае нелинейных уравнений может потребоваться использование численных методов или аппроксимаций для нахождения переходной функции.

После определения дифференциального уравнения звена и его решения, получаем аналитическое выражение для переходной функции. Это выражение может быть представлено в виде функции передаточной функции, частотного отклика или временной функции.

Установление переходной функции звена является важным шагом при анализе и проектировании динамических систем. Она позволяет определить, как система будет реагировать на различные входные сигналы во времени.