ПОЧЕМУ ДИФФЕРЕНЦИРУЕМАЯ ФУНКЦИЯ НЕПРЕРЫВНА
Дифференцируемая функция непрерывна, поскольку производная функции является ее локальным приращением. Если функция дифференцируема в точке, это означает, что существует касательная к кривой в этой точке, и функция гладко "склеивается" в этой точке без рывков и разрывов. Таким образом, если функция имеет производную во всех ее точках, она будет непрерывной.
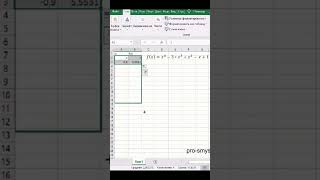
✓Дифференцируемая функция. Дифференциал - матан #032 - Борис Трушин
Математика без Ху%!ни. Непрерывность функции, точки разрыва.
Производная. Часть 5. Дифференцируемость и непрерывность функции. Несуществование производной.
Математический анализ, 5 урок, Непрерывность функции
Математика без Ху%!ни. Нахождение асимптот, построение графика функции.
Дифференциал функции