Как Определить Знак Интеграла

Интеграл – одно из основных понятий математического анализа, которое позволяет находить площадь под кривой или вычислять общий прирост функции в заданном интервале. При решении задач связанных с интегралами или исследовании их свойств, важно знать знак интеграла. Определить знак интеграла можно с помощью различных методов.

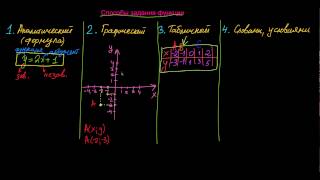
Первый метод позволяет определить знак интеграла, основываясь на интегральной сумме и точных значениях функции на заданном интервале. Если функция положительна на всем интервале интегрирования, то значение интеграла будет положительным, если функция отрицательна – интеграл будет отрицательным. Если на интервале присутствуют как положительные, так и отрицательные значения функции, необходимо провести расчет интегральной суммы, чтобы определить знак интеграла.

Второй метод основан на анализе графика функции и области под кривой. Если область находится выше оси абсцисс (x-оси), то знак интеграла будет положительным. Если область находится ниже оси абсцисс, то знак интеграла будет отрицательным.

Третий метод использует свойства неопределенного интеграла. Если значение функции на концах интервала интегрирования разных знаков, то интеграл будет отрицательным. Если значение функции на концах интервала одинаково, то интеграл будет равен нулю.

Важно понимать, что определение знака интеграла зависит от свойств функции и интервала интегрирования. При работе с конкретной функцией и интервалом, рекомендуется использовать все доступные методы определения знака интеграла для достоверных результатов.