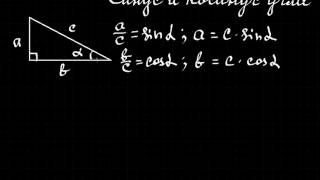Как Определить Предел Функции По Графику

Предел функции является одним из важных понятий в математическом анализе. Когда мы говорим о пределе функции по графику, мы рассматриваем, что происходит с функцией при стремлении аргумента к определенному значению.

Для определения предела функции по графику необходимо анализировать поведение функции вблизи заданной точки. График функции дает нам информацию о том, как функция меняется в окрестности этой точки.

Когда мы изучаем график функции, мы обращаем внимание на следующие моменты:

1. Наличие или отсутствие асимптот. Асимптоты могут быть вертикальными, горизонтальными или наклонными. Они определяют предельное поведение функции в бесконечности.

2. Значение функции вблизи заданной точки. Мы исследуем, как функция ведет себя при приближении к этой точке справа и слева.

3. Поведение функции вблизи заданной точки. Мы обращаем внимание на возможные разрывы, различные виды локальных экстремумов, значений функции около этой точки.

На основе анализа графика функции мы можем делать предположения о пределе функции при стремлении аргумента к заданной точке. Однако для точного определения предела требуется более строгое математическое исследование, включающее использование определений и теорем математического анализа.