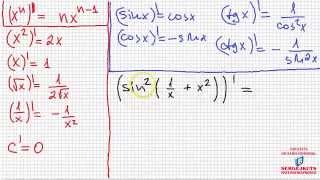КАК НАЙТИ ПРЕОБРАЗОВАНИЕ ФУРЬЕ ФУНКЦИИ

Преобразование Фурье является мощным инструментом в математике, который позволяет представить функцию в виде суммы гармонических колебаний различных частот. Это преобразование находит широкое применение в таких областях, как сигнальная обработка, теория информации, обработка изображений и многих других.

Чтобы найти преобразование Фурье функции, необходимо выполнить следующие шаги:

1. Выберите функцию, для которой вы хотите найти преобразование Фурье. Обозначим её как f(t).
2. Задайте диапазон значений, на котором будет вычисляться преобразование Фурье. Обычно это ограниченный интервал времени.
3. Разделите диапазон времени на равные интервалы и выберите достаточно малый шаг для точности вычислений.
4. Вычислите значения функции f(t) для каждого временного интервала.
5. Примените формулу преобразования Фурье к полученным значениям функции для каждого временного интервала.
6. В результате вы получите преобразование Фурье функции f(t), представленное в виде амплитуд и фаз различных гармонических компонент.

Преобразование Фурье важно для анализа различных типов функций и помогает понять их спектральные свойства. Оно позволяет выразить функцию через её спектр и обратно, что открывает большие возможности для решения задач в различных областях науки и техники.

Преобразования #7: амплитудный и фазовый спектры преобразования Фурье

Интеграл Фурье, преобразование Фурье

AGalilov: Преобразование Фурье \

Математика - быстрое преобразование Фурье и вейвлет-преобразование. Часть 1.

Ряд Фурье для функции x^2 и нахождение суммы трех числовых рядов.

Основы ЦОС: 18. Преобразование Фурье (ссылки на скачивание скриптов в описании)

Преобразование Фурье

Откуда взялся и что такое Ряд Фурье? Упрощенный вывод коэффициентов ряда

13.2 Разложение функции в ряд Фурье. Пример 1.