КАК НАЙТИ МНОЖЕСТВО ЗНАЧЕНИЙ СТЕПЕННОЙ ФУНКЦИИ

Степенная функция - это функция вида f(x) = ax^n, где a и n являются константами, а x - переменная. Множество значений степенной функции определяется диапазоном всех возможных значений функции.

Чтобы найти множество значений степенной функции, необходимо рассмотреть значения функции для различных значений переменной x. Для этого можно использовать следующий подход:

1. Выберите несколько значений для переменной x. Рекомендуется выбирать значения, которые покрывают различные области входных данных.
2. Подставьте выбранные значения переменной x в степенную функцию и вычислите соответствующие значения функции f(x).
3. Запишите все вычисленные значения функции в виде множества.

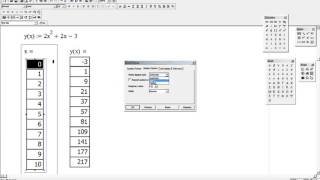
Например, рассмотрим функцию f(x) = 2x^2. Для нахождения множества значений этой функции:

1. Выберем несколько значений переменной x, например, x = -2, -1, 0, 1, 2.
2. Вычислим соответствующие значения функции f(x) при подстановке выбранных значений переменной x:
   • f(-2) = 2*(-2)^2 = 8
   • f(-1) = 2*(-1)^2 = 2
   • f(0) = 2*0^2 = 0
   • f(1) = 2*1^2 = 2
   • f(2) = 2*2^2 = 8
3. Множество значений степенной функции f(x) = 2x^2 будет {0, 2, 8}.

Таким образом, множество значений степенной функции зависит от выбранных значений переменной x и вычисленных значений функции. Найденное множество значений позволяет понять, какие значения может принимать функция при различных входных данных.

Как найти область определения функции? #shorts

Функция. Область определения функции. Практическая часть. 10 класс.

Множество значений функции #15

ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ 11 класс графики тригонометрических функций

Степенная функция, её свойства и график. Видеоурок 5. Алгебра 10 класс

Функция. Множество значений функции. Практическая часть. 10 класс.

Область значений функции

Множество значений тригонометрических функций

Степенная функция, ее свойства и график

Найти множество значений функции - Задача 1