КАК ДОКАЗАТЬ ЧТО ГРАФИКИ ФУНКЦИЙ НЕ ИМЕЮТ ОБЩИХ ТОЧЕК
Для доказательства того, что графики функций не имеют общих точек, мы можем использовать несколько различных методов. Один из них - это анализ функций и их характеристик, чтобы установить их взаимное положение на координатной плоскости.
Если у нас есть две функции, представленные графиками, мы можем изучить их поведение и проанализировать их производные. Если производные функций на всем их области определения имеют разные знаки, то это означает, что графики этих функций не пересекаются, и соответственно, у них нет общих точек.
Еще один способ доказать отсутствие общих точек между графиками функций - это анализ алгебраических выражений функций. Если мы можем привести выражения функций к эквивалентным формам и показать, что они противоречат друг другу, то мы можем сделать вывод о том, что графики функций не имеют общих точек.
Также можно обратиться к графическим методам. Построение графиков функций и их дальнейшее сравнение на координатной плоскости может помочь установить отсутствие общих точек. Если графики не пересекаются или не имеют общих сегментов, то можно сделать вывод, что у них нет общих точек.
В заключение, существует несколько методов для доказательства того, что графики функций не имеют общих точек. Анализ характеристик функций, исследование их производных, анализ алгебраических выражений и графический метод - все они могут быть использованы для достижения этой цели.
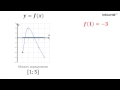
Постройте график функции, и определите, при каких значениях k график не будет иметь общих точек...
Точки пересечения графиков линейных функций. 7 класс.Образовательный
Графики функций. Задание №11 - Математика ОГЭ 2023 - Умскул
Точки пересечения графика линейной функции с координатными осями. 7 класс.
Линейная функция: краткие ответы на важные вопросы - Математика - TutorOnline
Свойства функции. Четность и нечетность функции. 10 класс.