КОГДА ФУНКЦИЯ ВЫПУКЛА ВВЕРХ
Функция является выпуклой вверх на некотором интервале, если любой отрезок, соединяющий две точки на графике функции, лежит выше самой функции, то есть график функции "выпукнут вверх".
Когда функция имеет выпуклую форму вверх, это означает, что её кривизна направлена вверх, поднимается вверх, как бы образуя "уголок". Это происходит, когда вторая производная функции положительна на всем диапазоне определения функции.
Выпуклость вверх - важное свойство функций, которое имеет множество приложений. Например, нахождение минимума или максимума функции, определение точек перегиба и построение гладких кривых.
Для определения выпуклости функции вверх можно использовать различные методы, включая геометрические и аналитические подходы. Ключевым фактором является знак второй производной функции: если она положительна, то функция выпукла вверх.
Наличие выпуклости вверх может быть полезным при оптимизации функций, при выборе маршрутов или решении задач на поиск экстремумов. Определение выпуклости функции позволяет делать выводы о её поведении и принимать решения на основе этого анализа.
Направления выпуклости. Тема
Из-за этого уравнения начался Палестино-Израильский конфликт
Семинар \
Выпуклость, вогнутость функции. 10 класс.
Семинар \
Математика без Ху%!ни. Исследование функции, график. Первая, вторая производная, асимптоты.
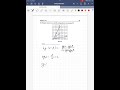
Найти интервалы выпуклости и точки перегиба графика функции
Свойства функции. Выпуклость вверх. Выпуклость вниз. Алгебра 7-11 класс.
Математический анализ, 14 урок, Выпуклость и вогнутость функции
Выпуклость графика функции Точки перегиба.