КАК СЧИТАТЬ ПРЕДЕЛЫ СЛОЖНЫХ ФУНКЦИЙ
Пределы сложных функций являются важным понятием в математике. Чтобы вычислить предел сложной функции, необходимо использовать соответствующие методы и правила.
Одним из методов является подстановка. Если функция представлена в виде комбинации других функций, можно заменить переменную внутренней функции и вычислить предел. Этот метод основан на правиле замены переменной и может быть полезен при работе со сложными выражениями.
Еще одним методом является использование арифметических свойств пределов. Существуют несколько правил, которые позволяют вычислять пределы сложных функций путем комбинирования их пределов. Эти свойства включают арифметические операции (сложение, вычитание, умножение, деление) и пределы элементарных функций.
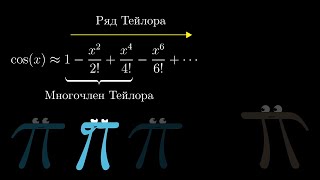
Если функция содержит более сложные операции, такие как экспонента или логарифм, необходимо использовать соответствующие свойства и правила для их вычисления. Это может включать применение правил дифференцирования или интегрирования, а также специальные тригонометрические или логарифмические идентичности.
Кроме того, иногда требуется применять более продвинутые методы, такие как правило Лопиталя, которое позволяет вычислять пределы функций, содержащих отношение производных.
Важно помнить, что вычисление пределов сложных функций требует достаточной математической подготовки и понимания соответствующих правил и методов. Расчеты могут быть довольно сложными и требовать тщательного анализа. Поэтому рекомендуется обратиться к учебникам или специализированным источникам для более подробной информации и примеров.
Матан за час. Шпаргалка для первокурсника. Высшая математика
Сложные пределы
✓ Предел функции. Определение предела функции \
27. Вычисление предела функции №1. Примеры 1-4
Как узнать просветленного?
Матан. Пределы для успешной сдачи зачёта - TutorOnline Математика