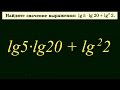КАК СЧИТАТЬ ГАММА ФУНКЦИЮ
Гамма-функция (обозначается как Γ) является важным математическим объектом, который широко используется в различных областях, включая математику, физику и статистику. Гамма-функция определена для всех комплексных чисел, кроме отрицательных целых.
Формула для вычисления гамма-функции выглядит следующим образом:
Γ(z) = ∫(0, ∞) x^(z-1) * e^(-x) dx
Важно заметить, что гамма-функция обладает множеством свойств, таких как рекурсивное соотношение, симметрия и формула для значений на полупрямой.
Для чисел, являющихся положительными целыми, гамма-функция определена следующим образом:
Γ(n) = (n-1)!
Однако, вычисление гамма-функции для произвольных комплексных чисел является нетривиальной задачей. Существуют различные алгоритмы и приближенные методы для расчета гамма-функции, такие как ряды Эйлера и формула Стирлинга.
Для вычисления гамма-функции в численном виде можно воспользоваться специализированными математическими библиотеками или программными пакетами, доступными на разных языках программирования.
Теперь, когда вы знакомы с гамма-функцией и способами ее вычисления, можете применять ее в своих математических исследованиях или задачах, где она может быть полезной.
#14. Гамма функция Эйлера. Основные понятия(1)
Эйлеровы интегралы (Гамма и Бета функции)
Гамма-функция и бета-функция: вывод основных соотношений
Элитная уединенная вилла в Ялте 🔝 Купить дом в Крыму
Вкратце о гамма-функции
ЗанятиеБиблФМ Гамма Функция