Как Решить Квадратное Неравенство С Помощью Графика Квадратичной Функции

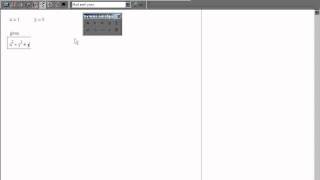
Квадратное неравенство может быть решено с помощью графика квадратичной функции. Для начала, нужно построить график этой функции. Квадратичная функция имеет вид f(x) = ax^2 + bx + c, где a, b и c - коэффициенты этой функции.

Чтобы построить график квадратичной функции, можно использовать пару точек и симметрию. Учитывая формулу f(x) = ax^2 + bx + c, выбираем значения x и вычисляем соответствующие значения функции f(x). Полученные точки поможет построить график, а симметрия относительно оси симметрии позволит дополнительно вычислить значения функции на противоположной стороне графика.

После построения графика квадратичной функции, решение квадратного неравенства состоит в определении области значений x, при которых функция f(x) удовлетворяет неравенству. Если неравенство имеет знак > или <, то необходимо определить область значений функции, находящуюся выше или ниже графика соответственно. Если неравенство имеет знак >= или <=, то решением будет область значений функции, находящаяся выше или ниже графика, включая точки пересечения.

После определения области значений x, решением квадратного неравенства будет множество чисел, удовлетворяющих этому условию.