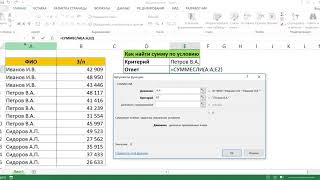
КАК НАЙТИ ПРОИЗВОДНУЮ ИНТЕГРАЛА
Производная интеграла — это основной инструмент математического анализа, позволяющий находить производные функций, заданных в виде интегралов. Для нахождения производной интеграла применяется фундаментальная теорема исчисления.
Чтобы найти производную интеграла, необходимо выполнить два важных шага. Во-первых, определить функцию, заданную интегралом, и задать пределы интегрирования. Во-вторых, использовать фундаментальную теорему исчисления, которая утверждает, что производная интеграла функции равна самой функции в точке, если она является непрерывной на всем интервале интегрирования.
Формально записывается следующим образом: если функция F(x) определена для всех x в пределах [a, b] и непрерывна на этом интервале, где a и b — пределы интегрирования, то интеграл от F(x) по переменной x соответствует функции G(x), определенной как
G(x) = ∫[a, x] F(t) dt,
где t — переменная интегрирования. В соответствии с фундаментальной теоремой исчисления, производная интеграла функции G(x) равна функции F(x) в точке x, то есть
G'(x) = F(x).
Таким образом, для нахождения производной интеграла, необходимо выполнить интегрирование заданной функции и затем взять производную от полученного результата.
Используя этот метод, можно находить производные интегралов и использовать их для решения широкого спектра задач в математике, физике, экономике и других науках.
Как найти производную определенного интеграла с переменным верхним пределом
Производная: секретные методы решения. Готовимся к ЕГЭ - Математика TutorOnline
Олегу Тинькову запрещён вход на Мехмат МГУ
Смысл интеграла и производной. В помощь студенту
ЗАЧЕМ НУЖНЫ ЭТИ... производные! Математика на QWERTY.
ВСЁ Чего Ты НЕ ЗНАЛ о ПРОИЗВОДНОЙ В Одном Вебинаре!
АЛГЕБРА С НУЛЯ — Что такое Производная?
Как устроен металлургический комбинат? - Экскурсия на Демидовский завод в Нижнем Тагиле