Как Найти Предел Функции С Бесконечностью

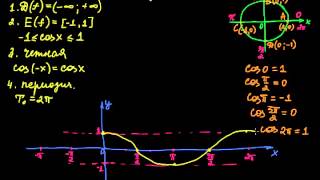
Предел функции с бесконечностью является важным понятием в математике. Он позволяет определить поведение функции при стремлении ее аргумента к бесконечности.

Для нахождения предела функции с бесконечностью необходимо анализировать ее асимптотическое поведение. Если функция имеет монотонное возрастание или убывание при стремлении аргумента к бесконечности, то ее предел можно найти путем простой замены переменных.

Если функция не является монотонной, то для нахождения предела можно использовать специальные приемы, такие как правило Лопиталя. Это правило позволяет заменить исходную функцию на отношение производных и повторить процесс до тех пор, пока не будет получен предел.

Также существуют другие методы нахождения предела, например, разложение функции в ряд Тейлора. При наличии разложения функции в ряд, можно аппроксимировать ее поведение при больших значениях аргумента и найти предел с помощью суммирования нескольких первых членов ряда.

Важно отметить, что для успешного нахождения предела функции с бесконечностью необходимо иметь определенные знания в области математического анализа и алгебры. Также стоит учитывать особенности конкретной функции и ее свойства. Поэтому решение подобных задач рекомендуется проводить под руководством опытного преподавателя или проконсультироваться со специалистом в данной области.