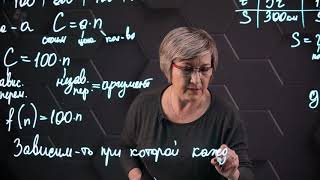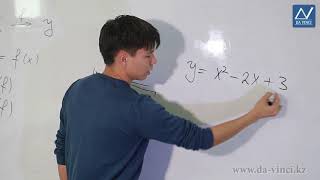Как Найти Отношение Приращения Функции К Приращению Аргумента

Отношение приращения функции к приращению аргумента в математическом анализе является важной концепцией для изучения изменений функций. Оно позволяет нам определить, как изменения входного значения (аргумента) влияют на значения функции.

Для того чтобы найти отношение приращения функции к приращению аргумента, используется производная функции. Производная функции показывает, как функция меняется при изменении аргумента. Она является коэффициентом пропорциональности между приращением функции и приращением аргумента.

Формально, отношение приращения функции к приращению аргумента определяется как предел производной функции по аргументу, когда приращение аргумента стремится к нулю:

отношение приращения функции к приращению аргумента

Где f'(x) обозначает производную функции f(x) по аргументу x.

Отношение приращения функции к приращению аргумента позволяет нам определить скорость изменения функции в каждой точке и выявить экстремумы функции — минимумы и максимумы.

Изучение отношения приращения функции к приращению аргумента полезно не только в математическом анализе, но и в других областях, таких как физика, экономика и программирование, где требуется анализ изменений и оптимизация задач.