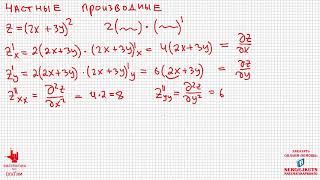Как Найти Критические Точки Квадратичной Функции

Чтобы найти критические точки квадратичной функции, необходимо сначала найти ее производную. Для этого возьмем формулу функции вида f(x) = ax^2 + bx + c, где a, b и c - коэффициенты квадратичной функции. Производная функции будет равна f'(x) = 2ax + b.

Далее, найдем корни уравнения f'(x) = 0. Для этого приравняем производную к нулю и решим полученное уравнение:

2ax + b = 0

Решение этого уравнения даст нам значения x, в которых производная равна нулю. Эти значения являются критическими точками квадратичной функции.

Также, чтобы определить, является ли критическая точка локальным минимумом или максимумом, можно использовать вторую производную. Если вторая производная больше нуля в критической точке, то это будет локальный минимум, а если вторая производная меньше нуля, то это будет локальный максимум.

Надеемся, что эта информация поможет вам в поиске критических точек квадратичной функции.