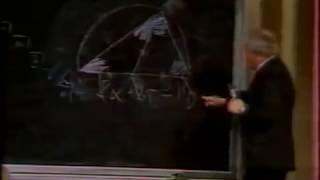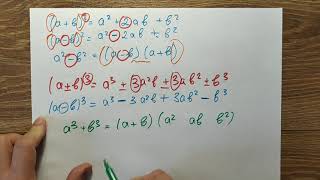Как Найти Косинус Х

Косинус - это одна из элементарных тригонометрических функций, которая широко применяется в математике, программировании и алгоритмах. Косинус угла можно найти с помощью математических формул и программных алгоритмов.

Для начала, необходимо знать значение угла, для которого нужно найти косинус. Угол может быть выражен в радианах или градусах. Ответ будет зависеть от того, в каких единицах измерения задан угол.

Если угол задан в радианах, то косинус угла можно найти с помощью математической функции cos(). Например, чтобы найти косинус угла х, нужно вычислить cos(х).

Если угол задан в градусах, то перед вычислением косинуса нужно преобразовать угол в радианы. Формула для перевода угла из градусов в радианы: радианы = градусы * (π/180), где π - математическая константа, приближенно равная 3.14159.

Программирование предлагает различные способы вычисления косинуса. В зависимости от языка программирования, вы можете использовать встроенные функции, библиотеки или написать свой алгоритм. Примеры кода для некоторых популярных языков:

Python:

import mathx = 3.14   # угол в радианахcos_x = math.cos(x)

Java:

import java.lang.Math;double x = 3.14;   // угол в радианахdouble cos_x = Math.cos(x);

C++:

#include double x = 3.14;   // угол в радианахdouble cos_x = std::cos(x);

JavaScript:

var x = 3.14;   // угол в радианахvar cos_x = Math.cos(x);

Таким образом, чтобы найти косинус угла х, нужно знать значение угла в радианах или градусах и использовать соответствующий алгоритм или функцию в выбранном языке программирования.