КАК НА ГРАФИКЕ ОТРАЖАЕТСЯ СВОЙСТВО НЕПРЕРЫВНОСТИ ФУНКЦИИ У Х2
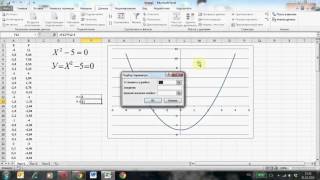
Функция y = х² является непрерывной на всей числовой прямой. Это означает, что график функции не имеет перерывов, разрывов или скачков. Непрерывность функции х² означает, что значение функции меняется плавно и непрерывно по мере изменения значения аргумента.
На графике функции y = х² это свойство непрерывности проявляется в виде гладкой кривой линии, которая не имеет пропусков или острых угловых точек. График начинается в точке (0,0) и направлен вверх, с тем, как значение х повышается, значение у также повышается, что создает плавное и непрерывное изменение.
Непрерывность функции у х² означает, что можно выбрать любой точку на графике и существует окрестность вокруг этой точки, где функция также определена и непрерывна. Никакие разрывы или перерывы не возникают, что делает график удобным для анализа и демонстрации свойств функции.
В целом, график функции у х² иллюстрирует свойство непрерывности, показывая, что функция может быть определена и непрерывна на всей числовой прямой, без каких-либо разрывов или пропусков. Это помогает нам понять и визуально представить, как функция х² ведет себя при изменении значения аргумента х.
✓ Неравенство треугольника - Ботай со мной #126 - Борис Трушин
Математика без Ху%!ни. Непрерывность функции, точки разрыва.
Задание 23 из ОГЭ Построение графиков функций с модулем - Математика
Математический анализ, 5 урок, Непрерывность функции
Математика без Ху%!ни. Нахождение асимптот, построение графика функции.
Матан за час. Шпаргалка для первокурсника. Высшая математика
Как создать графику в стиле Melodysheep с помощью нейросети Midjorney и After Effects