Что Такое Полиномиальная Функция

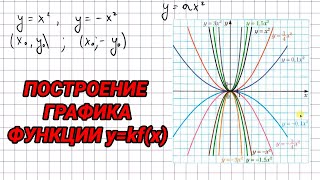
Полиномиальная функция - это функция вида y = a_n*x^n + a_{n-1}*x^{n-1} + ... + a_1*x + a_0, где a_i - коэффициенты, а n - степень полинома.

Степень полинома указывает на наивысшую степень переменной x, которая встречается в данном уравнении. Коэффициенты a_i могут быть любыми действительными числами. Важно отметить, что степень полинома определяет его поведение и форму.

Полиномиальные функции широко применяются в математике и науке. Они помогают моделировать различные явления и процессы. Коэффициенты полинома могут быть использованы для нахождения корней, экстремумов, а также для аппроксимации данных.

Степень полинома влияет на его алгоритмическую сложность. Например, полиномы с маленькой степенью могут быть решены аналитически, в то время как полиномы высокой степени требуют численных методов для решения.

Выводы из полиномиальных функций могут быть полезными в различных областях, таких как физика, экономика, инженерия и компьютерные науки. Понимание полиномиальных функций играет важную роль в развитии математической аналитики и алгоритмического мышления.