Что Такое Ограниченность Функции

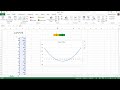
Ограниченность функции означает, что значения функции в определенной области ограничены сверху или снизу. Конкретнее, функция считается ограниченной, если существуют числа M и N, такие что для всех значений x в этой области выполняется условие: M ≤ f(x) ≤ N.

Если функция ограничена сверху, то все ее значения находятся ниже определенного числа. А если функция ограничена снизу, то все ее значения находятся выше определенного числа. Если функция ограничена и сверху, и снизу, то она называется ограниченной.

Ограниченность функции имеет важное значение в математике и приложениях. Например, ограниченность функции позволяет нам определить ее максимальное и минимальное значение, что полезно при решении оптимизационных задач или определении глобального экстремума функции.

Важно отметить, что для большинства математических функций ограниченность зависит от области определения функции. Функция может быть ограниченной в одной области, но не в другой.

В заключение, ограниченность функции относится к свойству функции, означающему, что ее значения ограничены сверху или снизу. Это свойство играет важную роль в математике и имеет множество приложений в различных областях.