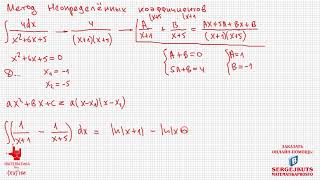Почему Дифференциал Функции Можно Использовать В Приближенных Вычислениях

Дифференциал функции может быть использован в приближенных вычислениях в связи с его возможностью представления локального поведения функции в окрестности определенной точки. Используя дифференциал, мы можем получить линейное приближение функции вблизи этой точки, что позволяет нам упростить сложные вычисления и получить приближенный результат.

Одной из основных причин использования дифференциала в приближенных вычислениях является его связь с понятием производной. Дифференциал функции определен как произведение производной функции и изменения аргумента. Это позволяет нам аппроксимировать изменение значения функции при небольшом изменении аргумента, чтобы получить более простую и понятную формулу для вычислений.

Дифференцирование функции также позволяет нам находить экстремумы функции. Используя дифференциал и условие равенства нулю производной, мы можем найти такие точки, в которых функция достигает своего максимума или минимума, что имеет важное значение в оптимизации и поиске решений в реальных приложениях.

При использовании дифференциала в приближенных вычислениях нужно учитывать, что он является линейным приближением функции в окрестности определенной точки. При больших изменениях аргумента или вдали от выбранной точки линейное приближение может быть неточным. Поэтому для достижения более точных результатов следует использовать малые изменения аргумента и проверять полученное приближение на адекватность.