КАКОЙ УГОЛ ОБРАЗУЕТ С ОСЬЮ АБСЦИСС КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ ПРОВЕДЕННАЯ В УКАЗАННОЙ ТОЧКЕ
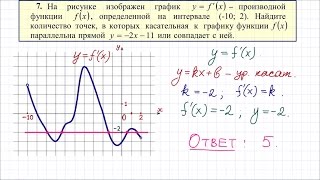
Угол, образуемый касательной к графику функции, проведенной в указанной точке, с осью абсцисс, зависит от наклона этой касательной. Если касательная горизонтальна (сдвигается параллельно оси абсцисс), угол между касательной и осью абсцисс составляет 0 градусов.
Если касательная имеет положительный наклон (поднимается вверх), то угол будет положительным и меньше 90 градусов. Чем круче наклон, тем больше угол между касательной и осью абсцисс.
Если же касательная имеет отрицательный наклон (опускается вниз), то угол будет отрицательным и больше -90 градусов. Здесь также справедливо, что чем круче наклон, тем больше угол между касательной и осью абсцисс.
Геометрический смысл производной. Уравнение касательной
Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.
ЕГЭ по математике / База / Задание 14 / Производные и касательные / Простое объяснение / Решу ЕГЭ
10 класс, 43 урок, Уравнение касательной к графику функции
Уравнение касательной в точке. Практическая часть. 2ч. 10 класс.
ЕГЭ 2017 Профильный №7 найти производную в точке касания #7
Прямая y=8x+11 параллельна касательной к графику функции y=x^2+7x-7. Найдите абсциссу точки касания.
Касательная к графику функции в точке. 10 класс.
Математика без Ху%!ни. Уравнение касательной.
ЗАЧЕМ НУЖНЫ ЭТИ... производные! Математика на QWERTY.