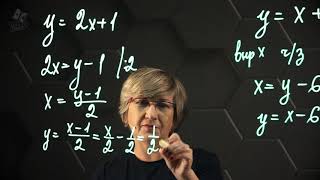Как Расположены Графики Прямой И Обратной Функции

Графики прямой и обратной функции имеют взаимосвязанную природу. Прямая функция представляет собой график, где каждому значению аргумента соответствует единственное значение функции.

Обратная функция, наоборот, является графиком, где каждому значению функции соответствует единственное значение аргумента. Таким образом, если у функции F(x) есть обратная функция, она обозначается как F^(-1)(x).

Графики прямой и обратной функции располагаются относительно оси абсцисс и оси ординат. На графике прямой функции, точки представляются парами (x, y), где x - аргумент функции, а y - значение функции.

Обратный график функции, напротив, представляет точки (y, x), где y - значение функции, а x - соответствующее значение аргумента.

Обратная функция имеет особенность — она является отражением прямой функции относительно прямой y = x. То есть, если на прямой функции точка (x,y) лежит на графике, то на обратной функции точка (y,x) будет лежать на ее графике.

Таким образом, графики прямой и обратной функции симметричны относительно прямой y = x. Если прямая функция стремится к бесконечности или имеет асимптоты, то обратная функция будет пересекать или подходить к асимптотам соответственно.