КАК ОПРЕДЕЛИТЬ ИНТЕРВАЛ НА КОТОРОМ ФУНКЦИЯ ПРИНИМАЕТ ПОЛОЖИТЕЛЬНЫЕ ЗНАЧЕНИЯ
Для определения интервала, на котором функция принимает положительные значения, необходимо проанализировать ее график и найти участки, где она находится выше оси x.
Первым шагом следует вычислить корни функции - это те значения аргумента, при которых функция равна нулю. Затем можно построить таблицу знаков, указав знак функции в различных интервалах между этими корнями. Если значению функции соответствует положительный знак (+), то это интервал, где функция принимает положительные значения.
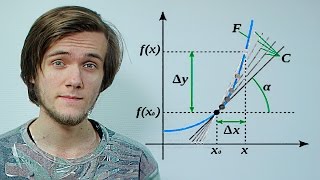
Также возможно использование производной функции для определения интервалов, на которых она положительна. Для этого необходимо найти точки, в которых производная функции равна нулю или не существует, и провести анализ знаков производной на соответствующих интервалах. Если производная положительна (+), то функция возрастает и принимает положительные значения на данном интервале.
Итак, для определения интервала, на котором функция принимает положительные значения, необходимо анализировать корни функции и ее производной, и проводить анализ знаков. Такой подход позволяет определить интервалы, на которых функция положительна и на которых можно ожидать положительных значений функции.
МЕТОД ИНТЕРВАЛОВ. БОЛЬШЕ НИКАКИХ ПОДСТАНОВОК ДЛЯ ОПРЕДЕЛЕНИЯ ЗНАКОВ!
Свойства функции. Промежутки возрастания и убывания функции. 10 класс.
Нахождение значений аргумента (х), при которых функция примимает положительные значения
Функции и их свойства #6
Свойства функции.
Свойства функции. Промежутки знакопостоянства. 10 класс.
Значения, при которых ф-ция положительная или отрицательная
Линейная функция: краткие ответы на важные вопросы - Математика - TutorOnline
✓Дифференцируемая функция. Дифференциал - матан #032 - Борис Трушин
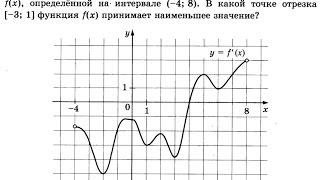
13A.1 Найдите промежутки возрастания и убывния функции f(x), заданной графиком