КАК НАЙТИ НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЕ ФУНКЦИИ ТРИГОНОМЕТРИЧЕСКОЙ

Функции тригонометрических выражений являются часто встречающимися в математике, и нахождение их наибольшего и наименьшего значений может быть полезным для различных задач. Вот основные шаги для нахождения наибольшего и наименьшего значения функции тригонометрической.

1. Определите диапазон значений переменной. Прежде чем искать экстремумы функции, необходимо определить диапазон значений переменной, в котором вы хотите найти наибольшее и наименьшее значение функции.

2. Найдите критические точки. Критические точки функции - это точки, где производная функции равна нулю или не определена. Чтобы найти критические точки функции тригонометрической, возьмите производную функции и приравняйте ее к нулю. Решите полученное уравнение, чтобы найти значения переменной, соответствующие критическим точкам.

3. Определите конечные точки интервала. Если функция определена на конечном интервале, необходимо проверить, достигается ли наибольшее или наименьшее значение на границах интервала. Подставьте значения граничных точек в функцию и сравните результаты.

4. Используйте теорему Ферма. Теорема Ферма гласит, что если функция имеет экстремум внутри интервала, то производная функции в этой точке должна быть равна нулю или не существовать. Если вы нашли критическую точку функции, убедитесь, что значение производной в этой точке равно нулю или не определено.

5. Проверьте значения наибольшего и наименьшего экстремумов. Сравните значения функции в критических точках, на границах интервала и в любых других точках, которые вы считаете важными, чтобы определить наибольшее и наименьшее значение функции.

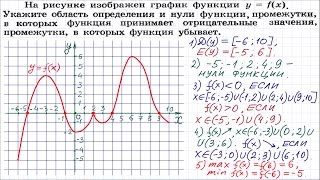
6. Проверьте еще раз. Всегда рекомендуется проверить свои результаты, проанализировав функцию с использованием графика или компьютерной программы для визуализации функций, если это возможно. Таким образом, вы можете убедиться, что находите наибольшее и наименьшее значение функции тригонометрической правильно и полно.

Производная. Наибольшее и наименьшее значение тригонометрической функции. 10-11 класс

Работает на 100%. Бесценные Советы Татьяны Черниговской !!!

Задание 12 ЕГЭ по математике #45

Математический анализ, 13 урок, Наибольшее и наименьшее значение функции на отрезке

Наибольшее и наименьшее значение функции. 10 класс.

Найдите наибольшее и наименьшее значения тригонометрического выражения 1-4cosa. Как решить? Просто!

Как найти наибольшее и наименьшее значения выражения cos α+√3 sin α. Тригонометрия. Простое решение

Наибольшее и наим. значения функции на отрезке

Наибольшее и наименьшее значение функции. Практическая часть. 10 класс.

9. ФНП. Наибольшее и наименьшее значение функции 2-х переменных в замкнутой области.