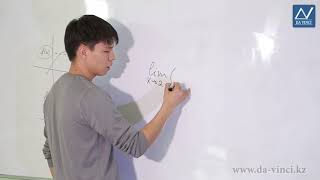Как Найти Градиент Функции Двух Переменных

Градиент функции двух переменных используется для определения направления наибольшего возрастания функции в заданной точке.

Для нахождения градиента функции двух переменных необходимо вычислить две частные производные этой функции по каждой переменной.

Предположим, что у нас есть функция f(x, y), где x и y - переменные. Чтобы найти градиент этой функции, нужно вычислить следующие частные производные:

∂f/∂x - частная производная функции f по переменной x,

∂f/∂y - частная производная функции f по переменной y.

Значения ∂f/∂x и ∂f/∂y будут составлять компоненты градиента функции f(x, y).

Таким образом, градиент функции f(x, y) будет представлен как вектор:

∇f = (∂f/∂x, ∂f/∂y).

Этот вектор указывает направление наибольшего возрастания функции в заданной точке.

Нахождение градиента функции двух переменных может быть полезным, например, при оптимизации функций или в задачах машинного обучения.