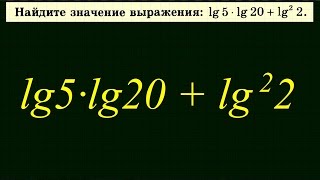Как Внести Функцию Под Знак Дифференциала

Для внесения функции под знак дифференциала необходимо следовать определенным правилам. Операция внесения функции под знак дифференциала называется дифференцированием. Процесс дифференцирования позволяет найти производную функции по ее переменной.

Для внесения функции под знак дифференциала следует учитывать правила дифференцирования, которые зависят от типа функции. Например, для постоянной функции производная равна нулю, для степенной функции производная равна произведению показателя степени на коэффициент перед переменной, а для суммы функций производная равна сумме производных каждой функции.

Знание основных правил дифференцирования позволяет упростить процесс внесения функции под знак дифференциала. Например, для функции y = x^2, можно внести функцию под знак дифференциала следующим образом: dy = 2x*dx. Здесь dy - дифференциал функции y, dx - дифференциал переменной x.

Однако, при внесении функции под знак дифференциала необходимо быть внимательным и учитывать особенности каждой конкретной функции. Некоторые функции могут требовать использования более сложных правил дифференцирования, таких как правило дифференцирования сложной функции или правило дифференцирования обратной функции.

В заключение, внесение функции под знак дифференциала является важной операцией в математике, позволяющей найти производную функции. Соблюдение правил дифференцирования и учет особенностей каждой функции помогут выполнить эту операцию корректно и точно.