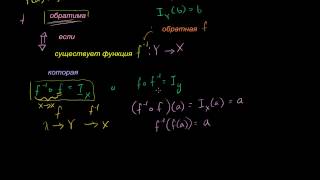КАК ОПРЕДЕЛИТЬ ВИД ИНТЕГРАЛА

Интеграл — один из основных понятий математического анализа. В зависимости от характеристик функции и области интегрирования, интеграл может быть классифицирован по видам. Определение вида интеграла позволяет выбрать подходящий метод интегрирования и решить задачу эффективно.

Одно из первых дел при определении вида интеграла — изучение функции под интегралом и ее свойств. Анализируйте непрерывность, непрерывное дифференцируемость, монотонность и периодичность функции. Эти характеристики могут указать на необходимость использования определенного типа интеграла.

Еще одним важным фактором, определяющим вид интеграла, является область интегрирования. Рассмотрите, имеет ли область симметрию или какие-либо особенности, которые могут упростить вычисление. Например, если область является симметричной относительно оси абсцисс или оси ординат, то интеграл может быть упрощен с помощью соответствующих свойств функции.

Также стоит выяснить, существуют ли какие-либо специальные формулы или методы, применимые для данного вида интеграла. Например, для определенных классов функций можно использовать замены переменных, интегрирование по частям или использование известных интегральных формул.

Некоторые основные виды интегралов включают определенные и неопределенные интегралы, криволинейные интегралы, поверхностные интегралы и объемные интегралы. Каждый вид имеет свои особенности и применяется в различных сферах математики, физики и инженерии.

Важно отметить, что определение вида интеграла требует понимания основных концепций математического анализа и интегрирования. Решение сложных задач интегрирования может потребовать использования специализированного программного обеспечения или консультации с экспертом в соответствующей области.

РАЗБИРАЕМ ИНТЕГРАЛЫ ЧАСТЬ I #математика #егэ #огэ #Shorts #задачиегэ #формулы

Определенный интеграл. 11 класс.

ИНТЕГРАЛ С НУЛЯ - определенный интеграл - ТАБЛИЦА ИНТЕГРАЛОВ - сумма Римана

Интеграл: Азы интегрирования. Высшая математика

Зачем нужен ИНТЕГРАЛ. Объяснение смысла

Определенные и неопределенные интегралы для чайников. Свойства интегралов.

Примеры решения определенных интегралов

Дмитрий Роде. Предпринимательство в условиях новой цифровой, политической и экономической реальности